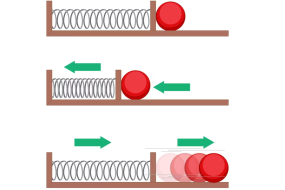
Sempre teve dificuldades em resolver problemas de Física envolvendo a conservação de energia mecânica? Pratique usando este simulador!
O simulador Conservação de energia mecânica apresentado abaixo mostra a dinâmica de um objeto pontual, representado pela bolinha vermelha, que segue um caminho unidimensional com variações de altura. Ao passar por diferentes alturas, é possível observar transformações que ocorrem entre as energias cinética e potencial gravitacional. Você também pode adicionar uma mola ao final do percurso, para observar o efeito da energia potencial elástica no movimento da bolinha.
Exemplo
Uma partícula de massa $m = 2,5$ kg desliza com velocidade uniforme de 7,5 m/s em um caminho retilíneo. O final do percurso possui uma elevação de 2,5 m em relação a parte retilínea, como mostrado abaixo. Encontre a velocidade da partícula na parte retilínea superior do percurso. Considere $g = 10$ m/s$^2$. Clique no botão Iniciar simulação para ver a transformação de parte da energia cinética em energia potencial gravitacional.
Usando a lei da conservação da energia, resolvemos esse tipo de problema considerando que a energia mecânica total $E$, isto é, a soma da energia cinética $E_c$ com a energia potencial $E_P$ é a mesma em todos os pontos do percurso. Assim, chamando a energia total na parte inferior de $E_1$ e a energia total na parte superior de $E_2$, temos então que
ou seja,
Ec1+Ep1=Ec2+Ep2 mv212+mgh1=mv222+mgh2 v212+gh1=v222+gh2 7,522+10×0,5=v222+10×3 v2=√7,52−50 v2=2,5 m/s,que é o velocidade da partícula na parte superior que você encontra ao rodar a simulação acima.
Problema 1
Uma partícula de massa 5 kg é lançada com velocidade de 3 m/s em direção a uma mola com constante elástica de 200 N/m. Qual é a deformação máxima que a mola sofre ao ser comprimida pela partícula?
Como não há variações de altura na trajetória, podemos ignorar o papel da energia potencial gravitacional. No ponto de partida temos então apenas energia cinética. Quando a mola está na sua deformação máxima, a velocidade da partícula é zero, de forma que sobra apenas energia potencial elástica. Igualando as duas, temos então que
Ec=Epe mv22=kx22 mv2=kx2 5×32=200x2 x2=45200 x2=940 x=47,4 cmProblema 2
Uma partícula de massa 3 kg é lançada com velocidade de 2 m/s em um plano. Parte da região a ser atravessada pela partícula, com comprimento de um metro e meio, possui um coeficiente de atrito cinético de 0,3. A partícula consegue atravessar essa região com atrito? Se sim, qual a sua velocidade após atravessá-la? Se não, quantos centímetros a partícula consegue se mover na região com atrito?
A presença de uma região com atrito fará a energia cinética da partícula (ou parte dela) se dissipar em energia térmica. A energia perdida por dissipação na região com atrito é dada pelo módulo do trabalho da força de atrito:
W=Fd W=μmgd W=0,3×3×10×1,5 W=13,5 JPara saber se a partícula consegue atravessar a região com atrito, basta saber se a energia cinética inicial é maior do que a energia dissipada por atrito, que é de 13,5 J. Calculando, temos
Ec=mv22 Ec=3×42 Ec=6 JNão há, assim, energia cinética suficiente para vencer o trabalho realizado pela força de atrito. Dessa forma, a partícula não consegue atravessar essa região com atrito. Para saber quantos centímetros a partícula consegue percorrer na região com atrito, igualamos a energia cinética inicial com a energia dissipada por atrito ao se deslocar por uma distância $d$:
mv22=μmgd 6=0,3×3×10×d 9d=6 d≈67 cm
Referências