Neste artigo derivamos as equações do movimento usadas no app Conservação de Energia Mecânica a partir do formalismo Lagrangeano da mecânica clássica.

Considere o movimento de uma partícula de massa $m$ restrito a uma dada trajetória $y = y(x)$. Sobre a partícula agem a força peso $P$ e, em determinadas regiões do percurso, força de atrito $F_{at}$ e força elástica $F_{el}$ de uma mola, como mostrado na Fig. 1. Conhecidas as condições iniciais $x(0) = x_0$ e $v(0) = v_0$, mostraremos aqui como encontrar a posição e a velocidade em qualquer instante $t > 0$.

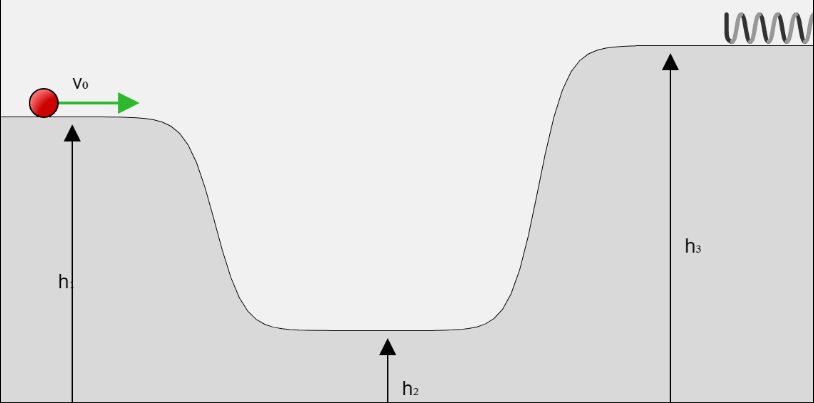
Consideraremos o formalismo lagrangeano da mecânica clássica, a maneira mais fácil de chegar nas equações do movimento. A energia cinética da partícula é dada por

$$T = \dfrac{m}{2} (\dot{x}^2 + \dot{y}^2). \tag{1}$$

Como o movimento está restrito a uma trajetória unidimensional, podemos eliminar a variável $y$ considerando a restrição

$$y = y(x). \tag{2}$$

Nesse caso, a energia cinética fica dependendo apenas de $x$ e de $\dot{x}$:

$$T = \dfrac{m\dot{x}^2}{2} [1 + y^\prime(x)^2]. \tag{3}$$

A energia potencial $U$ do sistema possui dois termos: energia potencial gravitacional e energia potencial elástica, de forma que escrevemos

$$U = mgy(x) + \dfrac{k(x - x_M + l_0)^2}{2}H(x - x_M + l_0), \tag{4}$$

onde $y(x)$ é a altura da partícula em relação a um dado referencial, $H$ é a função degrau de Heaviside, $x_M$ é a posição da extremidade direita da mola, mantida fixa, e $l_0$ é o seu comprimento no repouso. No app, $l_0 = 70$ cm. $H$ entra na equação (4) porque a força elástica começa a atuar no objeto apenas quando ele está em contato com mola, isto é, sempre que $x > x_M - l_0$.

De posse das equações (3) e (4), chegamos no lagrangeano do sistema, ainda sem considerar a dissipação devido ao trabalho realizado pela força de atrito:

$$L = \dfrac{m\dot{x}^2}{2} [1 + y^\prime(x)^2] - mgy(x) - \dfrac{k(x - x_M + l_0)^2}{2}H(x - x_M + l_0). \tag{5}$$

Agora partimos da equação de Euler-Lagrange,

$$\dfrac{\partial L}{\partial x} - \dfrac{d}{dt} \left( \dfrac{\partial L}{\partial \dot{x}} \right) = 0, \tag{6}$$

para deduzir as equações no movimento. Para o primeiro termo do lado esquerdo da equação (6), podemos escrever

$$\dfrac{\partial L}{\partial x} = m\dot{x}^2y^\prime(x)y^{\prime\prime}(x) - mgy^\prime(x) - k|x - x_M + l_0|H(x - x_M + l_0). \tag{7}$$

Já para o segundo termo, o cálculo das derivadas parcial e total levam a

$$\dfrac{d}{dt} \left( \dfrac{\partial L}{\partial \dot{x}} \right) = 2m\dot{x}^2y^\prime(x) y^{\prime\prime}(x) + m\ddot{x}[1 + y^\prime(x)^2] .\tag{8}$$

Juntando as equações (7) e (8), chegamos na seguinte equação:

$$[1 + y^\prime(x)^2]\ddot{x} + y^\prime(x) y^{\prime\prime}(x) \dot{x}^2 + gy^\prime(x) + \dfrac{k}{m}|x - x_M + l_0|H(x - x_M + l_0) = 0. \tag{9}$$

Essa equação possui dois termos não lineares, o que implica que, muito provavelmente, não deve haver uma solução exata para ela. E ainda falta incluir o efeito da dissipação por atrito.

Já esperando por uma solução numérica, vamos dividir essa EDO de segunda ordem em duas de primeira ordem. Considerando que $\dot{x} = v$ e que $\ddot{x} = \dot{v}$, chegamos no sistema de EDOs abaixo:

$$\begin{matrix} \dot{x} = v\\ [1 + y^\prime(x)^2]\dot{v} = - y^\prime(x) y^{\prime\prime}(x) v^2 - gy^\prime(x) - \dfrac{k}{m}|x - x_M + l_0|H(x - x_M + l_0). \end{matrix} \tag{10}$$

A última etapa que falta fazer é incluir o efeito do atrito. No app, o coeficiente de atrito $\mu_c$ só existe na região plana central, centralizada em $x = x_a$ com largura de $l_a$. Sabemos que a força de atrito cinético é dada, em módulo, por

$$F_{at} = \mu_c m g. \tag{11}$$

Assim, inserindo $F_{at}/m$ no sistema (10), chegamos finalmente no conjunto de EDOs por trás do simulador Conservação de Energia Mecânica:

$$\begin{matrix} \dot{x} = v\\ [1 + y^\prime(x)^2]\dot{v} = - y^\prime(x) y^{\prime\prime}(x) v^2 - gy^\prime(x) - \dfrac{k}{m}|x - x_M + l_0|H(x - x_M + l_0) - \mu_c g \Pi\left( \dfrac{x-x_a}{l_a} \right) \text{sign(v)}, \end{matrix} \tag{12}$$

onde $\Pi$ é a função retângulo, ou função Pi de Heaviside, definida por

$$\Pi\left( \dfrac{x}{a} \right) = \left\{ \begin{matrix} 0, & \text{ se} & |x| > \frac{a}{2}\\ \frac{1}{2} & \text{ se} & |x| = \frac{a}{2}\\ 1 & \text{ se} & |x| < \frac{a}{2}. \end{matrix} \right. \tag{13}$$

$\Pi$ aparece no sistema (12) para delimitar a dissipação por atrito dentro do intervalo $x_a - l_a/2 < x < x_a + l_a/2$.

No aplicativo, o sistema de equações (12) é resolvido numericamente pelo método de Runge-Kutta de quarta ordem com passo de integração temporal 0,0035h (em unidades de segundos), onde h pode ser escolhido pelo usuário com valores possíveis entre 1 e 10. Isso deve levar a um erro numérico relativo a algo em torno de 0,025%.